EX: And
x > -3 and x < 5
And means that both have to be true. That is, x must be both bigger than -3 and smaller than 5.
So if we were to graph the above inequality, it would look like this:

Notice, it’s the space between -3 and 5—where x is both bigger than -3 and less than 5.
EX: Or
x ≥ 4 or x < 0
Or means that at least one has to be true. That is, x must be either greater than 4 or less than 0.
So is we were to graph the above compound inequality, it would look like this:

So the solutions are everything except 0 and the numbers between 0 and 4.
You may also have to solve compound inequalities, like this:
EX: Solving
3x – 1 > 5 and –x – 6 > 1
You can solve each separately.
3x – 1 > 5
+1 +1
3x > 6
3 3
x > 2
-x + 6 > 1
-6 -6
-x > -5
x < 5
So we have x > 2 and x < 5
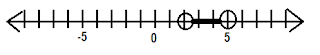
Sometimes, the inequalities are joined like this:
-3 < x + 5 ≤ 8
In these cases, we assume that we are using and instead of or.
In these cases, you can separate the two inequalities and solve them individually:
-3 < x + 5 and x + 5 ≤ 8
Or you can solve the two simultaneously—solve for x in the middle.
-3 < x + 5 ≤ 8
-5 -5 -5
-8 < x ≤ 3
ABSOLUTE VALUES
An absolute value |x| gives the positive value of x. For example:
|3| = 3 because 3 is already positive
|-3| = 3 as well.
When we have absolute values in inequalities, we end up with compound inequalities.
EX: Absolute value
|x| ≤ 4
Let’s think about this inequality. The x clearly can’t be anything bigger than 4. But it also can’t be anything smaller than -4, because the absolute value of something like -5 would be 5.
So we can rewrite this inequality as
x ≤ 4 and x ≥ -4
or you can write it as -4 ≤ x ≤ 4
EX: Solving with an absolute value
5 < |x| - 2
+2 +2
7 < |x| Now we use that trick
-7 < x < 7
EX: Solving with an absolute value
4 < |x – 1| Here, we use the absolute value trick first, since the 1 is inside the absolute value
-4 < x – 1 < 4 Then solve.
No comments:
Post a Comment